Blackjack Card Combinations
Posted : admin On 7/23/2022(From Proceedings of the Fifth National Conference on Gambling and Risk Taking, Vol. X: The Blackjack Papers, University of Nevada, Reno, 1982)
© Arnold Snyder 1980
- As a Blackjack hand frequency is approximately 4.8% (see the table Two Card Hand Frequency), the payout of 1:1 will increase house edge by 2.3% and the payout of 6:5 - by 1.4%. The first rule (1:1) is only rarely found, while the second (6:5) can be found at some tables with a single deck blackjack game.
- Blackjack Variations. American Blackjack; Blackjack Switch; Casino Blackjack; European Blackjack; Free Blackjack; High Stakes Blackjack; Live Dealer Blackjack; Multi-hand Blackjack; Multi-player Blackjack; Online Blackjack; Real Money Blackjack; Single Deck Blackjack; Pontoon; Blackjack on Mobile. Mobile Blackjack; Android Blackjack; iPad Blackjack; iPhone Blackjack.
- Every player is dealt two cards at the beginning of a round of blackjack so this chart tells you the percentage of getting different categories of hands. A natural blackjack is only 4.8%, which essentially is an ace dealt with a ten card straight off the initial deal. Normally the odds are 3 to 2 and you would win $3 for every $2 wagered.
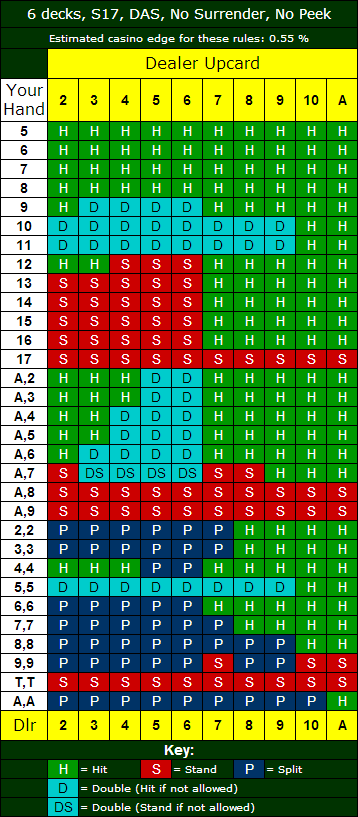
- However, with so many different combinations possible, it’s hard to remember the best move for each scenario. Below we’ve added some free blackjack strategy charts to get you started.
Blackjack is played with a conventional deck of 52 playing cards and suits don’t matter. 2 through 10 count at face value, i.e. A 2 counts as two, a 9 counts as nine. Face cards (J,Q,K) count as 10. Ace can count as a 1 or an 11 depending on which value helps the hand the most.
[Acknowledgements: This paper was originally published in 1980. Subsequent correspondence with a number of blackjack experts--notably Stanford Wong, Ph. D., Peter Griffin, Ph. D., and Bob Fisher--has led me to revise the original formula and some of the original recommendations.]
The currently employed methods of computing playing strategy indices involve high-speed computers and complex programs based on the intricate complexities of probability mathematics. Though it has been almost 20 years since the first such programs were written, there is still disagreement among experts as to the most accurate methods of approximation.
To approximate blackjack strategy tables, I will take an algebraic approach, which is far simpler than computerized methods. It has been shown that playing strategy indices cannot be accurately determined by linear methods, but it is also true that current computerized methods are imprecise approximations. I am not convinced that current computer methods are more accurate than algebraic methods, in conjunction with certain linear assumptions.
My calculations are based on Peter Griffin's Theory of Blackjack1. Anyone unfamiliar with this work will assuredly not fully comprehend my methods. I will refer often to Griffin's methods, and will neither redefine nor explain those concepts that Griffin presents so clearly in his book. I do not mean to imply that Griffin in any way suggests in his book that his calculations be used as I will use them. The theories and methods herein are my own.
For those who are unfamiliar with computer methods of obtaining strategy indices, consider the math involved in computing a single hit-stand decision. Assume a single-deck game, Vegas Strip rules, with the player holding a total of 16 versus a dealer upcard of ten (hereinafter, any 10, J, Q, K will be written 'X'). The player is using the Dubner (Hi-Lo) count to keep track of the cards, and wishes to know at which 'true count' or 'count-per-deck' standing becomes the preferred strategy.
In this counting system, 2s, 3s, 4s, 5s, and 6s are assigned a value of +1 as they are removed from the deck. Ten-valued cards and aces are counted as -1. Count-per-deck is defined as the running count divided by the fractional proportion of one deck remaining. The first consideration in solving this problem is to realize that a player total of 16 may be composed of any number of different combinations of cards. There are, in fact, 145 different combinations of cards which would total hard 16 (See Chart #1, Appendix).
Naturally, one would be more likely to be holding a combination of X-6 than a hand of A-A-A-A-2-2-2-2-4. In fact, if dealt in that order, one would simply have split A-A. In another permutation, one would surely have stood on A-2-A-A-A-2-2, a soft 20, and the decision of how to play such an unlikely 9-card total of 16 would not have presented itself. Dealt as in the table, 4-2-2-…-A, one might conceivably face this decision.
It must be determined which of these 145 combinations are relevant to the decision, according to all the rules, procedures and options of the game. For each of these specific hands, one may determine the precise advantage of hitting or standing simply by considering the outcome of every possible series of player and dealer draws (and down-cards). By properly weighting each of these possibilities, according to how probable each hand and series of events is, one would determine basic strategy for the decision of whether to hit or stand on 16 versus X.
The amount of math involved in any single basic strategy decision is vast. That a highly accurate basic strategy was originally, and painstakingly, computed on crude adding machines is phenomenal.2 Naturally, short-cuts were taken in devising this strategy. Computers made possible precise calculations, but even after decades of mathematical research, there is still dispute over basic strategy.
Julian Braun3 says to split 2-2 vs. 3 in the single-deck game. Stanford Wong4 says to hit. Both are highly qualified mathematicians and computer programmers. Peter Griffin has computed the only 100% accurate single-deck basic strategy, but this strategy has not yet been published. Dr. Griffin informs me that on this particular strategy decision, Braun's recommendation to split 2-2 vs. 3 is the correct play.
We still have not considered the calculations involved in computing the count-per-deck at which a Dubner count system player would stand on 16 vs. X, rather than follow basic strategy. There is a precise mathematical method which will accurately determine this index number. One need only determine all of the possible deck compositions which would indicate each of the various true counts, then compute the expectation from every possible series of draws, down cards, etc., for each relevant combination of cards totaling 16, weighting each outcome to reflect its probability. The enormity of this task prohibits its being carried out, even by computer. The cost of computing such accurate indices far exceeds any card counter's, system seller's, or casino's stake in the game.
Again, mathematicians have resorted to short-cuts. Rather than analyze every possible deck composition that would indicate each specific count-per-deck, the accepted method is to analyze carefully chosen representative deck compositions. The accuracy of indices so determined is dependent on how closely the chosen decks reflect true probability.
There exist now, and have always been, differences of opinion regarding the best method of choosing a count representative deck. Lawrence Revere,5 it has been pointed out by Julian Braun,6 erred in failing to remove neutral (0 value) cards when composing his deck subsets. The computer-derived indices, therefore, were all based on decks with an abnormally high proportion of neutral cards. A similar error had been made by Braun years earlier in composing decks for the Dubner count indices for Thorp's 1966 Beat the Dealer.7 Braun later corrected this error, and recomputed these indices, the corrected version of which appear in his How to Play Winning Blackjack.
Stanford Wong's indices for the Dubner count differ from Braun's. Wong argues that his method of choosing a representative deck will produce more accurate indices.8 Griffin points out the inherent limited accuracy of determining indices by using these artificially composed decks to represent all possible deck subsets. To quote Griffin, '…even the most carefully computerized critical indices have an element of faith in them.' What Baldwin, et al., once did with adding machines to determine basic strategy is now being done with computers to determine playing strategy indices.
A simpler and, I believe, equally accurate approach, would be to precisely compute one set of strategy tables, by which any counting system could be measured, and indices calculated. On pages 74 to 85 of Theory of Blackjack, Peter Griffin provides the precise information necessary to calculate such indices by algebraic methods.
The formula is simple. Divide the favorability of no action (i.e., not hitting, not splitting, etc.) by the total effect of the count-valued cards. To obtain count-per-deck, simply multiply this by the sum of the squares of the points counted per deck. One thus obtains the critical index at which the action pivots from favorable to unfavorable, or vice-versa. (One must also account for the sum of the removed card(s)' point values, and adjust this count to reflect 'count-per-deck').
The complete formula looks like this:
(mp/i) + t = count-per-deck for altering strategy
m = 'mean' or 'favorability', which Griffin presents in the eleventh column of his tables. It is necessary to reverse the sign (+/-) of Griffin's 'mean', since he is quoting the favorability of making the action (hitting, etc.)
p = sum of the squares of the 'points' counted per deck. Example: for the Dubner system, counting +1 for 2, 3, 4, 5, 6; and -1 for X and A; p=40. For Hi-Opt II counting +1 for 2, 3, 6, 7; +2 for 4, 5; and -2 for X; p=112. Simply multiply the sum of the squares of the points of the 13 different cards by 4 (for the four suits).
i = the 'inner product' of the count system's point values and the effects of removal. These effects are listed in Griffin's tables. He also explains the method of calculating the inner product (p. 44).
t = the sum of the point values of the removed cards, adjusted for 'true' count-per-deck.
(This formula is identical to the one in my original paper except that here I recommend p = the sum of the squares of the point values. In the original paper I recommended p = the absolute sum of the point values. For any level one count, such as the Dubner/Hi-Lo count, as will be shown in this paper, either valuation of p will produce identical indices, since 12 = 1. The few discrepancies between the charts in this paper and those of the original paper are due to slight computational and typographical errors in the original charts, discovered by Bob Fisher.
I also published a correction sheet for the first paper, which advised multiplying by 'a', where a = the average point value of a counted card. With the new formula, this methodology is not advised. Both the original formula and this revised variation of it will produce identical indices for level one count systems and nearly identical indices for higher-level counts.
The new formula was developed by considering how the formula might best be applied to determining insurance indices, using Griffin's data on page 71 of Theory of Blackjack. Stanford Wong, who originally questioned the formula's validity for higher counts, pointed out to me that insurance indices were optimally calculated according to Bayesian principles, multiplying the point values of the various cards by their respective probability of being drawn. This inevitably produces a weighted count in which the ratio of the count values to one another is identical to the ratio of the respective values if all values of the count were simply squared.)
Example: 14 vs. A, single-deck, dealer stands on soft 17, using the Dubner count:
m = 18.85 (from column 11, p. 74, Theory of Blackjack)+ .44 (effect of removal of dealer's ace, p. 74, Theory of Blackjack)= 19.29 (+/-) = -19.29
p = 40 (sum of the squares of the Dubner point values)
i = -57.44 (Using the effects on p. 74, this figure is calculated for the 39 remaining point-valued cards, the dealer's ace having been removed.)
t = -1 (count-per-deck will be calculated according to a 51-card deck. With only the dealer's upcard removed, t will simply equal the point value of this card. To obtain a true count-per-52-card-deck, the single-deck index values, as per this paper, should be multiplied by 52/51 to account for the removal of the dealer's upcard. For the sake of simplicity, I have neglected this step, which is of minor practical significance to the player, whose count-per-deck approximations would be rounded to the nearest whole number anyway.)
Solving the formula:
(mp/i) + t = ((-19.29 x 40)/-57.44) + (-1) = 12.4
Thus, a player using the Dubner count should stand with a total of 14 versus ace at a count-per-deck of +12.4. On page 137 of How to Play Winning Blackjack, Julian Braun gives this index value as +12. On page 169 of Professional Blackjack (1980), Stanford Wong gives this index as +13. To demonstrate the effectiveness of this simple formula, I will produce all 38 hit-stand indices that Braun records on page 137 of his book. Wong's indices are on page 169 of his 1980 edition. So that my work may be easily checked, I will provide the single-deck values for m and i, with the dealer upcard removed, calculated as previously explained. In all cases, p = 40 and t = the point value of the dealer's upcard. Dealer stands on soft 17. (See charts #2 and #3, Appendix.)
Inserting the corresponding values from Charts #2 and #3 into the formula and solving, the complete single-deck hit-stand strategy table looks like this:
2| 3 | 4 | 5 | 6 | 7 | 8 | 9 | X | A | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 17 | -8.2 | |||||||||
| 16 | -9.0 | -10.4 | -12.2 | -13.5 | -13.6 | 9.9 | 8.6 | 4.1 | 0.0 | 6.9 |
| 15 | -5.4 | -6.8 | -8.5 | -9.6 | -9.8 | 11.6 | 10.9 | 7.2 | 4.2 | 8.2 |
| 14 | -3.1 | -4.6 | -6.3 | -7.5 | -7.7 | 15.4 | 12.4 | |||
| 13 | 0.0 | -1.4 | -3.2 | -4.8 | -4.5 | |||||
| 12 | 4.5 | 2.7 | 0.6 | -1.0 | -1.3 |
Comparing these indices to Braun's, my table as a whole is quite similar. Only 4 of the 38 algebraic indices differ from Braun's by more than 1 point, when the algebraic indices are rounded to whole numbers. All of these major differences are between double-digit indices, so are not highly significant from the standpoint of player expectation. Many players do not even memorize double-digit indices. Comparing the algebraic indices to Wong's, again the table is remarkably similar. If I round all algebraic indices to the nearest whole number, only one index value differs by two points. This index value is for 16 vs. 6, for which Wong gives -12, and which the algebraic formula determines to be -13.6.
I will point out that this formula will produce index values for some decisions for which no index value actually exists (such as, with this count, 14 vs. X). Such index values will for the most part be double-digit indices that would not contribute to any notable loss of profit because of their rare application.
Consider the problem of 'rounding' indices to whole numbers. Griffin has noted that this practice may introduce up to a 10% error in playing decisions. Few players can estimate a count-per-deck within fractions of a point, so indices are recorded as whole numbers. It I take liberty in rounding the algebraic indices to whole numbers in Wong's 'direction,' be it up or down (so that -13.6 may be rounded to -13), only 9 of the 38 algebraic indices differ from Wong's by one point, while the other 29 are the same. Note that Braun and Wong differ on 16 of these indices, four of them by 2 points.
One of Wong's points of contention with Braun's methodology is that Braun used linear methods (interpolation and extrapolation) to determine his four-deck strategy. Ironically, Braun's and Wong's four-deck strategies more closely resemble each other than do their single-deck strategies, where Braun's indices are not linear based. In his newsletter, Wong presents evidence that his methods of choosing his representative deck subsets are more accurate than Braun's.
Wong's arguments appear logical, but I have made no thorough comparative examination of their methods. Likewise, I would not recommend a player use algebraic indices instead of the computerized indices of a qualified expert like Julian Braun or Stanford Wong. I make no claim for the 'superiority' of the algebraic formula. It would be of practical use to a player who desired to play a count for which reliable strategy tables were not available, or were incomplete, or were available only at a price the player did not wish to pay.
In any case, considering the extreme approximation technique of creating a 'most likely' deck with a double-digit true count, I see no mathematical argument that -12, as per Wong, would be more accurate than the algebraically determined -13.6, and this is the most radical difference between any of Wong's and the algebraic single-deck hit-stand indices. What most surprises me is that a simple algebraic formula would so closely mimic the results of simulation-based data. (Readers familiar with The Blackjack Formula9 will note that I am essentially doing 'more of the same' to determine indices as I did to determine profit potential. Having reduced the problem to the fewest number of variables, I make simple algebraic assumptions.)
To demonstrate the uncanny precision of this mimicry, we may use the algebraic formula to determine indices for specific player hands versus dealer upcards. Wong, on page 171 of his book, quotes the 'two-card' hit-stand indices for the single-deck game, dealer stands on soft 17. For instance, both Wong's computer and the algebraic formula determine the critical index for 13 vs. 2 to be 0. However, Wong's 'two-card' table shows that for the player holding X-3 or 9-4, the correct index is +2. With 8-5 the index is -2. With 7-6: -3.
Applying the formula to X-3 vs. 2:
m = -1.28| (from Griffin, Theory of Blackjack,p. 85 | |
| -0.22 | (dealer's 2, p. 85) |
| +2.44 | (player's X, p. 85) |
| -0.16 | (player's 3, p. 85) |
As per Griffin (p. 86, Theory of Blackjack)
m = -1.28 + 51/49 (-0.22 + 2.44 - 0.16) = 0.86
Reverse sign (+/-): m = -0.86
i = -55.94 (after removing dealer's and player's cards)
t = 51/49 (+1 -1 +1) = 51/49
Solving the formula:
(-.86 x 40/-55.94) + 51/49 = 1.66
Similarly, solving each of the 'two-card' player hands, and comparing the results to Wong's:
Wong| Formula | ||
|---|---|---|
| Any 13 v. 2 | 0 | 0.0 |
| X-3 v. 2 | +2 | +1.7 |
| 9-4 v. 2 | +2 | +1.7 |
| 8-5 v. 2 | -2 | -2.5 |
| 7-6 v. 2 | -3 | -2.6 |
When comparing the algebraic results to hundreds of Wong's player 'total' and 'two-card' indices, including pair-splitting and double-down decisions, for both Wong's Hi-Lo and Halves counts (where p=44, and all values for both i and t were recalculated), where dealer both hits and stands on soft 17, the single-deck algebraic strategy is so similar to Wong's, it would take a computer simulation of many millions of hands to determine which strategy is actually superior.
The algebraic formula proves even more precise in mimicking computer-produced indices for multi-deck games, simply by weighting the removed cards according to diminishing effect. It is most convenient to simply calculate an infinite-deck strategy, and interpolate indices using the reciprocal of the number of decks (see Griffin, Theory of Blackjack, p. 115 and 127). There is very little difference between interpolated indices and indices calculated for the specific number of decks by the algebraic formula. Approximation of infinite-deck indices is quite a bit easier than calculating single-deck indices. The formula becomes simply mp/i, since t is irrelevant to an infinite number of decks.
m = Griffin's 11th column figure (=/-), with no adjustment for upcard removal
p = 40 (Hi-Lo count)
i = inner product of all 40 count-valued cards
We may further simplify by valuing p=10, and calculating i on the basis of each of the 10 different counted cards. These values are in Chart #4, Appendix.
Example: 14 vs. A
m = -18.85 (from Theory of Blackjack, p. 74, +/-)
p = 10
i = -14.47 (from Chart #4)
Solving mp/i = (-18.85 x 10)/-14.47 = 13.0
I will point out here that an 'infinite deck' is not only an impossibility, but that if one were keeping a running count of cards as they were removed from an infinite number of standard 52-card decks shuffled together, one's efforts would be pointless since 'true' count would inevitably always equal 0. The term 'infinite deck' is used simply to mean that the removal of any one card (dealer's upcard, in this example) will not in itself alter the ratio of the various cards to one another.
An infinite deck with a true count of +13, as per this example, means that an artificial deck would have to be created by removing 'low' cards and adding 'high' cards proportionately to obtain an 'infinite' deck in which the ratio of the 'low' cards to 'high' cards would indicate that for every 52 cards in the deck, an average count of +13 would be the sum of the assigned point values. In such an artificially composed deck, one's optimum strategy would be to stand on 14 v. A. In multi-deck games, infinite deck strategies are quite accurate, since the removal of any individual card has far less effect on deck composition than in a single-deck game.
The complete infinite-deck hit-stand table looks like this:
2| 3 | 4 | 5 | 6 | 7 | 8 | 9 | X | A | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 17 | --6.9 | |||||||||
| 16 | -9.1 | -10.3 | -10.8 | -12.0 | -13.7 | 7.4 | 5.9 | 3.6 | -0.6 | 7.9 |
| 15 | -5.9 | -7.1 | -7.8 | -8.8 | -9.5 | 9.4 | 8.6 | 6.7 | 3.3 | 8.9 |
| 14 | -3.9 | -5.2 | -5.8 | -6.9 | -7.5 | 17.4 | 13.0 | |||
| 13 | -0.9 | -2.2 | -3.1 | -4.5 | -4.6 | |||||
| 12 | 3.6 | 1.9 | 0.5 | -1.2 | -0.6 |

Comparing these indices with Wong's 4-deck indices (p. 173, Professional Blackjack, 1980 ed.), rounding to the nearest whole number, no algebraic index differs by more than one point. Note that 20 of Wong's single-deck indices change when computing for 4 decks, fifteen by 1 point, three by 2 points, and two by 3 points. The algebraic formula follows Wong's changes with notable precision. When I interpolate a 4-deck strategy chart (or compute a 4-deck chart by properly weighting the effects of the cards-either method producing almost identical results), the 4-deck indices are slightly closer to Wong's 4-deck indices than are these infinite-deck indices, and no algebraic index differs from either Wong's or Braun's 4-deck indices by more than one point.
Griffin's tables may thus be used to determine a highly accurate strategy for any balanced point-count system, for any hit-stand, hard or soft double, or pair-splitting decision, for any number of decks, for both soft 17 rules. Using the surrender data Griffin provides on pages 121 and 122 (Theory of Blackjack), one may easily calculate the favorability (m) for both early and late surrender; however, Griffin does not provide the effects of removal for either surrender option. It is not correct to use the effects on pages 74-85 to calculate the value of i for surrender decisions. The effect of removing any card on one's hit-stand or pair-splitting decision, for which Griffin supplies data, will naturally differ from the effect of removing that same card on one's surrender decision.

One other common rule variation for which data is not supplied in Griffin's tables is pair splitting when doubling after splitting is allowed. Nor does Griffin provide data on splitting X-X vs. upcards of 4, 5 or 6-occasional plays for single-deck players. Dr. Griffin has informed me that the effects of removal for doubling down on A-9 vs. 4, 5 and 6, respectively, may be used to calculate these indices with notable accuracy. For the most part, Griffin's 'Virtually Complete Strategy Tables' are aptly titled.
Over a weekend, using a programmable calculator, I devised relatively complete 1, 2, and 4-deck strategy tables for Hi-Opt II, Revere's Point Count, and Uston's Advanced Count. It was somewhat tedious, but consider the time and money required for computerized methods. I believe these indices to be as accurate as any devised to this point for any point count system.
I will not, by the way, make these strategy tables commercially available. In my opinion, no serious player should be without Griffin's book, which is all one needs to compute such tables. The calculations I have explained are not difficult. One need not comprehend the more advanced math of Griffin's appendices to produce strategy tables according to the algebraic method, though again, I will emphasize, one would need Griffin's book to understand and apply the methods I am proposing.
A few fine points: any time the inner product (i) is negative, as in all hit-stand decisions, the critical index for changing strategy will indicate the point at which the action (i.e., hitting) pivots from favorable to unfavorable. Any time i is a positive number, as in most double-down and pair-splitting decisions, the critical index will indicate the point at which the action pivots from unfavorable to favorable. Chart #4 (Appendix) also gives the values of i for the most common doubling and pair-splitting decisions, Dubner count, p = 10, infinite deck.
Note that of the 37 most common double-down and split decisions, only 8-8 vs. X has a negative value for i, accurately indicating that for this decision, one will be determining the critical index at which the action becomes unfavorable. This infinite-deck index value, by the way, works out to be +5.2-comparing it favorably to both Wong's and Braun's 4-deck index value of +6.
Of the 37 infinite-deck doubling and splitting indices that may be easily calculated from Chart #5, using Griffin's tables for m, 26 round off precisely to Wong's 4-deck decisions. The algebraic method consistently produces index values comparable to computer-derived values for every decision I have tested-and I have tested many examples for every type of decision for which Griffin provides data. The indices that Wong changes when switching from his Hi-Lo to Halves counts likewise change when calculated thus algebraically.
I will note that a major difference between Wong's and Braun's indices, relative to the algebraic indices, is that Wong's methodology produces indices which correspond more precisely to indices produced via algebraic and linear assumptions. An objective examination of both Wong's and Braun's methods will, no doubt, be done in time. Should Braun's methods prove superior, then certain assumptions regarding algebraic error, depending on how Wong erred, may be made. Should Wong's methods prove to be superior, the theoretical implications are interesting.
In my original version of this paper, I stressed the major value of the algebraic formula would be for players who play in single-deck games, and whose current systems do not provide 'two-card' hit-stand decisions. From Griffin's table of 'Average Gains for Varying Basic Strategy' (p. 30, Theory of Blackjack), note that some hit-stand decisions alone are worth more than all pair-splitting decisions combined.
Some of these most valuable hit-stand decisions, such as the 13 vs. 2 previously analyzed, can be most efficiently played in single-deck games by using two-card decisions. It occurred to me that a player might potentially realize more profit in a single-deck game from learning two-card decisions for 16 vs. X, and both 12 and 13 vs. 2 and 3, than by learning all hard and soft doubling and pair-splitting decisions combined.
From the practical point of view, the only pair-splitting indices worth learning at all are splitting X-X vs. 4, 5, and 6. Of the doubling indices, only 10 and 11 vs. X, and 11 vs. ace are worth varying basic strategy for. A sophisticated player would memorize strategy indices according to potential profitability.
Since publication of my original paper, Peter Griffin has pointed out to me that the method of computing the gain from learning two-card indices as opposed to learning a single non-composition-dependent index for any decision is to calculate the correlation of the count system for each two-card hand to obtain a weighted average correlation for the decision, and comparing this to the correlation of the non-composition-dependent decision. Learning two-card indices is not, alas, practical, as such strategies will not raise the simple correlation of the count system sufficiently to warrant the increased memory effort.
I will note, however, that the recommendations of most systems developers to learn and utilize strategy tables for pair-splitting, surrender, and most double-down decisions are ill-considered, since the potential gains from such strategies are so negligible that most players should not chance making errors by attempting to employ such indices. The information provided in Theory of Blackjack, in conjunction with the formula presented in this paper, is more than sufficient to develop a count strategy for any balanced count system, as complete as any player could practically apply at the tables.
Until system sellers analyze and incorporate into their systems the wealth of information in Griffin's Theory of Blackjack, serious players should study this book themselves.
As I pointed out in The Blackjack Formula, the financial opportunities of blackjack, as a 'get-rich-quick' racket, are largely imaginary. The very effective casino countermeasures, which Thorp had predicted in his 1962 edition of Beat the Dealer were inevitable, have been largely ignored by most systems sellers since. Casinos have learned that it is in their interest to keep the blackjack profit myths alive. However, many casinos do not offer games exploitable to any profitable end by card counting. The profit potential of even the best games available in this country can only be realistically taken advantage of by highly knowledgeable players with sizeable bankrolls. A present-day professional card counter must enter the game with the same attitude, preparation, inside information, and ability to withstand fluctuations, as any investor of sizeable amounts of money on Wall Street.
In his bibliography for Theory of Blackjack, Peter Griffin states that if he were to recommend one book, and one book only, on the subject, it would be the 1966 edition of Thorp's Beat the Dealer. My recommendation for a second book on this subject would be, without question, Griffin's Theory of Blackjack. For the serious blackjack student, Griffin's work stands alone as a detailed analysis of the probabilities and possibilities of applied blackjack strategy.
Chart 1, All Combinations of Cards that Total Hard Sixteen
X-6
| 7-5-3-A | 5-5-3-2-A | |
| X-5-A | 7-5-2-2 | 5-5-2-2-2 |
| X-4-2 | 7-5-2-A-A | 5-5-2-2-A-A |
| X-4-A-A | 7-5-A-A-A-A | 5-5-2-A-A-A-A |
| X-3-3 | 7-4-4-A | 5-5-4-4-3 |
| X-3-2-A | 7-4-3-2 | 5-4-4-2-A |
| X-3-A-A-A | 7-4-3-A-A | 5-4-4-A-A-A |
| X-2-2-2 | 7-4-2-2-A | 5-4-3-3-A |
| X-2-2-A-A | 7-4-2-A-A-A | 5-4-3-2-2 |
| X-2-A-A-A-A | 7-3-3-3 | 5-4-3-2-A-A |
| 9-7 | 7-3-3-2-A | 5-4-3-A-A-A-A |
| 9-6-A | 7-3-3-A-A-A | 5-4-2-2-2-A |
| 9-5-2 | 7-3-2-2-2 | 5-4-2-2-A-A-A |
| 9-5-A-A | 7-3-2-2-A-A | 5-3-3-3-2 |
| 9-4-3 | 7-3-2-A-A-A-A | 5-3-3-3-A-A |
| 9-4-2-A | 7-2-2-2-2-A | 5-3-3-2-2-A |
| 9-4-A-A-A | 7-2-2-2-A-A-A | 5-3-3-2-A-A-A |
| 9-3-3-A | 6-6-4 | 5-3-2-2-2-2 |
| 9-3-2-2 | 6-6-3-A | 5-3-2-2-2-A-A |
| 9-3-2-A-A | 6-6-2-2 | 5-3-2-2-A-A-A-A |
| 9-3-A-A-A-A | 6-6-2-A-A | 5-2-2-2-2-A-A-A |
| 9-2-2-2-A | 6-6-A-A-A-A | 4-4-4-4 |
| 9-2-2-A-A-A | 6-5-5 | 4-4-4-3-A |
| 8-8 | 6-5-4-A | 4-4-4-2-2 |
| 8-7-A | 6-5-3-2 | 4-4-4-2-A-A |
| 8-6-2 | 6-5-3-A-A | 4-4-4-A-A-A-A |
| 8-6-A-A | 6-5-2-2-A | 4-4-3-3-2 |
| 8-5-3 | 6-5-2-A-A-A | 4-4-3-3-A-A |
| 8-5-2-A | 6-4-4-2 | 4-4-3-2-2-A |
| 8-5-A-A-A | 6-4-4-A-A | 4-4-3-2-A-A-A-A |
| 8-4-4 | 6-4-3-3 | 4-4-2-2-2-2 |
| 8-4-3-A | 6-4-3-2-A | 4-4-2-2-2-A-A |
| 8-4-2-2 | 6-4-3-A-A-A | 4-4-2-2-A-A-A-A |
| 8-4-2-A-A | 6-4-2-2-2 | 4-3-3-3-3 |
| 8-4-A-A-A-A | 6-4-2-2-A-A | 4-3-3-3-2-A |
| 8-3-3-2 | 6-4-2-A-A-A-A | 4-3-3-3-A-A-A |
| 8-3-3-A-A | 6-3-3-3-A | 4-3-3-2-2-2 |
| 8-3-2-2-A | 6-3-3-2-2 | 4-3-3-2-2-A-A |
| 8-3-2-A-A-A | 6-3-3-2-A-A | 4-3-3-2-A-A-A-A |
| 8-2-2-2-2 | 6-3-3-A-A-A-A | 4-3-2-2-2-2-A |
| 8-2-2-2-A-A | 6-3-2-2-2-A | 4-3-2-2-2-A-A-A |
| 8-2-2-A-A-A-A | 6-3-2-2-A-A-A | 4-2-2-2-2-A-A-A-A |
| 7-7-2 | 6-2-2-2-2-A-A | 3-3-3-3-2-2 |
| 7-7-A-A | 6-2-2-2-A-A-A-A | 3-3-3-3-2-A-A |
| 7-6-3 | 5-5-5-A | 3-3-3-3-A-A-A-A |
| 7-6-2-A | 5-5-4-2 | 3-3-3-2-2-2-A |
| 7-6-A-A-A | 5-5-4-A-A | 3-3-3-2-2-A-A-A |
| 7-5-4 | 5-5-3-3 | 3-3-2-2-2-2-A-A |
| 3-3-2-2-2-A-A-A-A |
Chart 2, m (Favoribility) 51-card Deck, Dealer Upcard Removed (+/-)
Dealer Stands on Soft 17
2
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | X | A | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 17 | 9.34 | |||||||||
| 16 | 18.94 | 23.34 | 28.38 | 32.81 | 29.59 | -8.15 | -7.61 | -3.36 | -0.68 | -13.71 |
| 15 | 12.87 | 16.90 | 21.50 | 25.18 | 22.53 | -12.25 | -11.37 | -7.03 | -4.31 | -16.68 |
| 14 | 7.07 | 10.47 | 14.28 | 17.61 | 15.51 | -12.58 | -19.29 | |||
| 13 | 1.50 | 3.89 | 7.13 | 10.41 | 8.51 | |||||
| 12 | -4.43 | -2.33 | 0.55 | 3.22 | 1.49 |
Chart 3, i (Inner Product), Dubner Count, 51-card Deck, Dealer Upcard Removed
Dealer Stands on Soft 17
2
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | X | A | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 17 | -51.72 | |||||||||
| 16 | -75.91 | -81.75 | -86.08 | -90.59 | -81.22 | -32.88 | -35.44 | -32.60 | -26.44 | -69.76 |
| 15 | -81.00 | -86.54 | -90.57 | -95.03 | -83.08 | -42.08 | -41.84 | -39.08 | -33.08 | -72.44 |
| 14 | -68.95 | -74.35 | -78.46 | -82.70 | -71.46 | -32.72 | -57.44 | |||
| 13 | -58.54 | -64.14 | -68.17 | -71.80 | -61.42 | |||||
| 12 | -50.42 | -55.63 | -59.37 | -62.86 | -52.95 |
Chart 4, i (Inner Product), Dubner Count, Infinite Deck (p=10)
Dealer Stands on Soft 17
2
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | X | A | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 17 | -12.80 | |||||||||
| 16 | -19.32 | -20.95 | -22.51 | -23.72 | -19.97 | -8.22 | -8.86 | -8.15 | -7.73 | -17.44 |
| 15 | -20.43 | -21.99 | -23.45 | -24.65 | -21.34 | -10.82 | -10.46 | -9.77 | -9.47 | -18.21 |
| 14 | -17.32 | -18.78 | -20.24 | -21.38 | -18.31 | -8.18 | -14.47 | |||
| 13 | -14.69 | -16.13 | -17.48 | -18.46 | -15.67 | |||||
| 12 | -12.63 | -13.97 | -15.15 | -16.03 | -13.42 | |||||
| 11 | 16.45 | 15.04 | 12.92 | 10.88 | 23.78 | |||||
| 10 | 16.07 | 20.40 | 18.63 | 15.63 | 10.10 | 26.53 | ||||
| 9 | 15.50 | 16.61 | 18.03 | 19.00 | 18.08 | 20.17 | 17.52 | |||
| AA | 31.83 | 30.89 | 29.58 | 28.42 | 40.11 | |||||
| 99 | 21.15 | 22.40 | 25.15 | 28.49 | 24.22 | 8.96 | 15.88 | 11.51 | 8.87 | |
| 88 | -9.42 | 13.03 | ||||||||
| 66 | 17.50 | 21.23 | 18.75 |
REFERENCES
- Griffin, Peter: Theory of Blackjack (Las Vegas: Huntington Press, 1979)
- Baldwin, Cantey, Maisel, McDermott: 'The Optimum Strategy in Blackjack,' (Journal of the American Statistical Society, Vol. 51, 1956)
- Braun, Julian H.: How to Play Winning Blackjack (Chicago: Data House, 1980)
- Wong, Stanford: Professional Blackjack (revised) (La Jolla, CA: Pi Yee Press, 1980)
- Revere, Lawrence: Playing Blackjack as a Business (Seacaucus, NJ: Lyle Stuart, 1971, '73, '75, '77)
- Braun, Julian H.: The Development and Analysis of Winning Strategies for the Casino Game of Blackjack (Chicago: Julian Braun, 1974)
- Thorp, Edward O.: Beat the Dealer (New York: Random House, 1962, '66)
- Wong, Stanford: Blackjack World (La Jolla, CA: Pi Yee Press, October 1980)
- Snyder, Arnold: The Blackjack Formula (Berkeley, CA: R.G. Enterprises, 1980)
[Note: If you are the kind of math geek, like me, who can actually make it to the end of an article like this, you may be interested in The Blackjack Shuffle Tracker's Cookbook, in which I use algebra to calculate the value of various casino-style shuffles to a shuffle-tracker, and got results that overturned the conventional wisdom of the time. — Arnold Snyder]
Return to Arnold Snyder's Professional Gambling Library
Return to Blackjack Forum Online Home
By Ion Saliu, Founder of Blackjack Mathematics
I. Probability, Odds for a Blackjack or Natural 21
II. House Edge on Insurance Bet at Blackjack
III. Calculate Double-Down Hands
IV. Calculate Blackjack Pairs: Strict or Mixed Ten-Cards
V. Free Blackjack Resources, Basic Strategy, Casino Gambling Systems
1.1. Calculate Probability (Odds) for a Blackjack or Natural 21
First capture by the WayBack Machine (web.archive.org) Sectember (Sect Month) 1, 2015.I have seen lots of search strings in the statistics of my Web site related to the probability to get a blackjack (natural 21). This time (November 15, 2012), the request (repeated 5 times) was personal and targeted directly at yours truly:
- 'In the game of blackjack determine the probability of dealing yourself a blackjack (ace face-card or ten) from a single deck. Show how you arrived at your answer. If you are not sure post an idea to get us started!'
Oh, yes, I am very sure! As specified in this eBook, the blackjack hands can be viewed as combinations or arrangements (the order of the elements counts; like in horse racing trifectas).
1) Let's take first the combinations. There are 52 cards in one deck of cards. There are 4 Aces and 16 face-cards and 10s. The blackjack (or natural) can occur only in the first 2 cards. We calculate first all combinations of 52 elements taken 2 at a time: C(52, 2) = (52 * 51) / 2 = 1326.
We combine now each of the 4 Aces with each of the 16 ten-valued cards: 4 * 16 = 64.
The probability to get a blackjack (natural): 64 / 1326 = .0483 = 4.83%.
2) Let's do now the calculations for arrangements. (The combinations are also considered boxed arrangements; i.e. the order of the elements does not count).
We calculate total arrangements for 52 cards taken 2 at a time: A(52, 2) = 52 * 51 = 2652.
In arrangements, the order of the cards is essential. Thus, King + Ace is distinct from Ace + King. Thus, total arrangements of 4 Aces and 16 ten-valued cards: 4 * 16 * 2 = 128.
The odds to get a blackjack (natural) as arrangement: 128 / 2652 = .0483 = 4.83%.
4.83% is equivalent to about 1 in 21 blackjack hands. (No wonder the game is called Twenty-one!)
Calculations for the Number of Cards Left in the Deck, Number of Decks
There were questions regarding the number of cards left in the deck, number of decks, number of players, even the position at the table.1) The previous probability calculations were based on one deck of cards, at the beginning of the deck (no cards burnt). But we can easily calculate the blackjack (natural) odds for partial decks, provided that we know the number of remaining cards (total), Aces and Ten-Value cards.
Let's take the situation heads-up: One player against the dealer. Suppose that 12 cards were played, including 2 Tens; no Aces out. What is the new probability to get a natural blackjack?
Total cards remaining (R) = 52 - 12 = 40
Aces remaining in the deck (A): 4 - 0 = 4
Ten-Valued cards remaining (T): 16 - 2 = 14
Odds of a natural: (4 * 14) / C(40, 2) = 56 / 780 = 7.2%
(C represents the combination formula; e.g. combinations of 40 taken 2 at a time.)
The probability for a blackjack is higher than at the beginning of a full deck of cards. The odds are exactly the same for both Player and Dealer. But - the advantage goes to the Player! If the Player has the BJ and the Dealer doesn't, the Player is paid 150%. If the Dealer has the blackjack and the Player doesn't, the Player loses 100% of his initial bet!
This situation is valid only for one Player against casino. Also, this situation allows for a higher bet before the round starts. For multiple players, the situation becomes uncontrollable. Everybody at the table receives one card in succession, and then the second card. The bet cannot be increased during the dealing of the cards. Hint: try as much as you can to play heads-up against the Dealer!
The generalized formula is:
Probability of a blackjack: (A * T) / C(R, 2)
2) How about multiple decks of cards? The calculations are not exactly linear because of the combination formula. For example, 2 decks, (104 cards):
~ the 2-deck case:
C(52, 2) = 1326
C(104, 2) = 5356 (4.04 times larger than total combinations for one deck.)
8 (Aces) * 32 (Tens) = 256
Odds of BJ for 2 decks = 256 / 5356 = 4.78% (a little lower than the one-deck case of 4.83%).
~ the 8-deck case, 416 total cards:
C(52, 2) = 1326
C(416, 2) = 86320 (65.1 times larger than total combinations for one deck.)
32 (Aces) * 128 (Tens) = 4096
Odds of BJ for 8 decks = 4096 / 86320 = 4.75% (a little lower than the two-deck situation and even lower than the one-deck case of 4.83%).
There are NO significant differences regarding the number of decks. If we round the figures, the general odds to get a natural blackjack can be expressed as 4.8%.
The advantage to the blackjack player after cards were played: Not nearly as significant as the one-deck situation.
3) The position at the table is inconsequential for the blackjack player. Only heads-up and one deck of cards make a difference as far the improved odds for a natural are concerned.
- Axiomatic one, let's cover all the bases, as it were. The original question was, exactly, as this: 'Dealing yourself a blackjack (Ace AND Face-card or Ten) from a single deck'. The calculations above are accurate for this unique situation: ONE player dealing cards to himself/herself. The odds of getting a natural blackjack are, undoubtedly, 1 in 21 hands (a hand consisting of exactly 2 cards).
- Such a case is non-existent in real-life gambling, however. There are at least TWO participants in a blackjack game: Dealer and one player. Is the probability for a natural blackjack the same – regardless of number of participants? NOT! The 21 hands (as in probability p = 1 / 21) are equally distributed among multiple game agents (or elements in probability theory). Mathematics — and software — to the rescue! We apply the formula known as exactly M successes in N trials. The best software for the task is known as SuperFormula (also component of the integrated Scientia software package).
- Undoubtedly, your chance to get a natural BJ is higher when playing heads-up against the dealer. The degree of certainty DC decreases with an increase in the number of players at the blackjack table. I did a few calculations: Heads-up (2 elements), 4 players and dealer (5 elements), 7 players and dealer (8 elements).
- The degree of certainty DC for 2 elements (one player and dealer), one success in 2 trials (2-card hands) is 9.1%; divided by 2 elements: the chance of a natural is 9.1% / 2 = 4.6% = the closest to the 'Dealing yourself a blackjack (Ace AND Face-card or Ten) from a single deck' situation.
- The chance for 5 elements (4 players and dealer), one success in 5 trials (2-card hands) is 19.6%; distributed among 5 elements, the degree of certainty DC for a blackjack natural is 19.6% / 5 = 3.9%.
- The probability for 8 elements (7 players and dealer), one success in 8 trials (2-card hands) is 27.1%; equally distributed among 8 elements, the degree of certainty DC of a blackjack natural is 27.1% / 8 = 3.4%.
- That's mathematics and nobody can manufacture extra BJ natural 21 hands... not even the staunchest and thickest card-counting system vendors! The PI... er, pie is small to begin with; the slices get smaller with more mouths at the table. Ever wondered why the casinos only offer alcohol for free — but no pizza?
1.2. Probability, Odds for a Blackjack Playing through a Deck of Cards
The probabilities in the first chapter were calculated for one trial. That is, the odds to get a blackjack in the first two cards. But what are the probabilities to get a natural 21 dealing an entire deck?
1.2.A. Dealing 2-card hands until the deck is dealt entirely
There are 52 cards in the deck. Total number of trials (2-card hands) is 52 / 2 = 26. SuperFormula probability software does the following calculation:- The probability of at least one success in 26 trials for an event of individual probability p=0.0483 is 72.39%.
1.2.B. Dealing 2-card hands in heads-up play until the deck is dealt entirely
There are 52 cards in the deck. We are now in the simplest real-life situation: heads-up play. There is one player and the dealer in the game. We suppose an average of 6 cards dealt in one round. Total number of trials in this case is equivalent to the number of rounds played. 52 / 6 makes approximately 9 rounds per deck. SuperFormula does the following calculation:- The probability of at least one success in 9 trials for an event of individual probability p=0.0483 is 35.95%.
You, the player, can expect one blackjack every 3 decks in heads-up play.
2. House Edge on the Insurance Bet at Blackjack
“Insurance, anyone?” you can hear the dealer when her face card is an Ace. Players can choose to insure their hands against a potential dealer's natural. The player is allowed to bet half of his initial bet. Is insurance a good side bet in blackjack? What are the odds? What is the house edge for insurance? As in the case of calculating the odds for a natural blackjack, the situation is fluid. The odds and therefore the house edge are proportionately dependent on the amount of 10-valued cards and total remaining cards in the deck.We can devise precise mathematical formulas based on the Tens remaining in the deck. We know for sure that the casino pays 2 to 1 for a successful insurance (i.e. the dealer does have Ten as her hole card).
We start with the most easily manageable case: One deck of cards, one player, the very beginning of the game. There is a total of 16 Teens in the deck (10, J, Q, K). The dealer has dealt 2 cards to the player and one card to herself that we can see exactly — the face card being an Ace. Therefore, 52 – 3 = 49 cards remaining in the deck. There are 3 possible situations, axiomatic one:
- 1) The player has 2 non-ten cards; there are 16 Teens in the deck = the favorable situations to the player if taking insurance. There are 49 – 16 = 33 unfavorable cards to insurance. However, the 16 favorable cards amount to 32, as the insurance pays 2 to 1. The balance is 33 – 32 = +1 unfavorable situation to the player but favorable to the casino (the + sign indicates a casino edge). In this case, there is a house advantage of 1/49 = 2%.
- 2) The player has 1 Ten and 1 non-ten card; there are 15 Teens remaining in the deck = the favorable situations to the player if taking insurance. There are 49 – 15 = 34 unfavorable cards to insurance. However, the 15 favorable cards amount to 30, as the insurance pays 2 to 1. The balance is 34 – 30 = +4 unfavorable situations to the player but favorable to the casino. In this case, there is a house advantage of 4/49 = 8%.
- This can be also the case of insuring one's blackjack natural: an 8% disadvantage for the player.
- This figure of 8% represents the average house edge regarding the insurance bet. I did calculations for various situations — number of decks and number of players.
- 3) The player has 2 Ten-count cards; there are 14 Teens in the deck = the favorable situations to the player if taking insurance. There are 49 – 14 = 35 unfavorable cards to insurance. However, the 14 favorable cards amount to 28, as the insurance pays 2 to 1. The balance is 35 – 28 = +7 unfavorable situations to the player but favorable to the casino. In this case, there is a house advantage of 7/49 = 14%. This is the worst-case scenario: The player should never — ever — even think about insurance with that strong hand of 2 Tens!
Believe it or not, the insurance can be a really sweet deal if there are multiple players at the blackjack table! Let's say, 5 players, the very beginning of the game. There is a total of 16 Teens in the deck (10, J, Q, K). The dealer has dealt 10 cards to the players and one card to herself that we can see exactly — the face card being an Ace. Therefore, 52 – (10 + 1) = 41 cards remaining in the deck. There are many more possible situations, some very different from the previous scenario:
- 1) The players have 10 non-ten cards; there are still 16 Tens in the deck = the favorable situations to the player if taking insurance. There are 41 – 16 = 25 unfavorable cards to insurance. However, the 16 favorable cards amount to 32, as the insurance pays 2 to 1. The balance is 25 – 32 = –7 favorable situation to the player but unfavorable to the casino (the – sign indicates a player advantage now). In this case, there is a house advantage of 7/41 = –17%. The Player has a whopping 17% advantage if taking insurance in a case like this one!
- 2) The players have 10 Ten-count cards; there are 6 Teens in the deck = the favorable situations to the player if taking insurance. There are 41 – 6 = 35 unfavorable cards to insurance. However, the 6 favorable cards amount to 12, as the insurance pays 2 to 1. The balance is 35 – 12 = +23 unfavorable situations to the player but favorable to the casino. In this case, there is a house advantage of 23/41 = 56%. This is the worst-case scenario: None of the players should ever even think about insurance with those strong hands of 2 Tens per capita!
- 3) Applying the wise aurea mediocritas adagio, there should be an average of 3 or 4 Teens coming out in 11 cards; thus, 12 or 13 Tens remaining in the deck. There are 41 – 13 = 28 unfavorable cards to insurance. However, the 12.5 favorable cards amount to an average of 25, as the insurance pays 2 to 1. The balance is 30 – 25 = +5 unfavorable situations to the player but favorable to the casino. In this case, there is a house advantage of 5/41 = 12%. Unfortunately, even if we consider averages, taking insurance is a repelling bet for the player.
Free Card Games 21 Blackjack
- A formula? It would look complicated symbolically, but it is very easy to follow.
- HA = house advantage
- R = cards remaining in the deck
- T = Tens remaining in the deck.
HA = {(R – T) – T*2} / R
where —
Blackjack Card Values
• Axiomatic one, buying (taking) insurance can be a favorable bet for all blackjack players, indeed. Of course, under special circumstances — if you see certain amounts of ten-valued cards on the table. The favorable situations are calculated by the formula above.
But, then again, a dealer natural 21 occurs about 5%- of the time — the insurance alone won't turn the blackjack game entirely in your favor.
3. Calculate Blackjack Double-Down Hands
Strictly-axiomatic colleague of mine, writing software leads me into new-ideas territory far more often than not. I discovered something new and intriguing while programming software to calculate the blackjack odds totally mathematically. By that I mean generating all possible elements and distinguishing the favorable elements. After all, the formula for probability is the rapport of favorable cases, FHow To Count Cards For Blackjack
, over total possible cases, N: p = F/N.Up until yours truly wrote such software, total elements in blackjack (i.e. hands) were obtained via simulation. Problem with simulation is incomplete generation. According to by-now famed Ion Saliu's Probability Paradox, only some 63% of possible elements are generated in a simulation of N random cases.
I tested my software a variable number of card decks and various deck compositions. I noticed that decks with lower proportions of ten-valued cards provided higher percentages of potential double-down hands. It is natural, of course, as Tens are the only cards that cannot contribute to a hand to possibly double down. However, the double-down hands provide the most advantageous situations for blackjack player. Indeed, it sounds like 'heresy' to all followers of the cult or voodoo ritual of card counting!
I rolled up my sleeves and performed comprehensive calculations of blackjack double-downs (2-card hands). The single deck is mostly covered, but the calculations can be extended to any number of decks.
At the beginning of the deck (shoe): Total combinations of 52 cards taken 2 at a time is C(52, 2) = 1326 hands. Possible 2-card combinations that can be double-down hands:
- 9-value cards AND 2-value cards: 4 9s * 4 2s = 16 two-card possibilities
- 8-value cards AND 2-value cards: 4 8s * 4 2s = 16 two-card configurations
- 8-value cards AND 3-value cards: 4 8s * 4 3s = 16 two-card possibilities
- 7-value cards AND 2-value cards: 4 7s * 4 2s = 16 two-card configurations
- 7-value cards AND 3-value cards: 4 7s * 4 3s = 16 two-card possibilities
- 7-value cards AND 4-value cards: 4 7s * 4 4s = 16 two-card configurations
- 6-value cards AND 3-value cards: 4 6s * 4 3s = 16 two-card configurations
- 6-value cards AND 4-value cards: 4 6s * 4 4s = 16 two-card combinations
- 6-value cards AND 5-value cards: 4 6s * 4 5s = 16 two-card possibilities
- 5-value cards AND 4-value cards: 4 5s * 4 4s = 16 two-card combinations
- 5-value cards AND 5-value cards: C(4, 2) = 6 two-card hands (5 + 5 can appear 6 ways).
- Ace AND 2-value cards: 4 As * 4 2s = 16 two-card combinations
- Ace AND 3-value cards: 4 As * 4 3s = 16 two-card possibilities
- Ace AND 4-value cards: 4 As * 4 4s = 16 two-card hands
- Ace AND 5-value cards: 4 As * 4 5s = 16 two-card possibilities
- Ace AND 6-value cards: 4 As * 4 6s = 16 two-card hands
- Ace AND 7-value cards: 4 As * 4 7s = 16 two-card combinations.
- Total possible 2-card hands in doubling down configuration: 262. Not every configuration can be doubled down (e.g. 4+5 against Dealer's 9 or A+2 against 7).
- We look at a double down blackjack basic strategy chart. Some 42% of the hands ought to be doubled-down (strongly recommended): 262 * 0.42 = 110. That figure represents 8% of total possible 2-hand combinations (1362), or a chance equal to once in 12 hands.
- The chance for double-down situations increases with an increase in tens out over the one third cutoff count. The probability for a natural blackjack decreases also — one reason the traditional plus-count systems anathema the negative counts. But what's lost in naturals is gained in double downs — and then some.
- A sui generisblackjack card-counting strategy was devised by yours truly and it beats the traditionalist plus count systems hands down, as it were.
- Be mindful, however, that nothing beats the The Best Casino Gambling Systems: Blackjack, Roulette, Limited Martingale Betting, Progressions. That's the only way to go, the tao of gambling.
4. Calculate Blackjack Pairs: Strict or Mixed Ten-Cards
The odds-calculating software I mentioned above (section III) also counts all possible blackjack pairs. The software, however, considers pairs to be two cards of the same value. In other words, 10, J, Q, K are treated as the same rank (value). My software reports data as this fragment (single deck of cards):Mixed Pairs: All 10-Valued Cards Taken 2 at a Time
Evidently, there are 13 ranks. Nine ranks (2 to 9 and Ace) consist of 4 cards each (in a single deck). Four ranks (the Tenners) consist of 16 cards. Total of mixed pairs is calculated by the combination formula for every rank. C(4, 2) = 6; 6 * 9 = 54 (for the non-10 cards). The Ten-ranks contribute: C(16, 2) = 120. Total mixed pairs: 54 + 120 = 174. Probability to get a mixed pair: 174 / 1326 = 13%.
Strict Pairs: Only 10+10, J+J, Q+Q, K+K
But for the purpose of splitting pairs, most casinos don't legitimize 10+J, or Q+K, or 10+Q, for example, as pairs. Only 10+10 , J+J, Q+Q, K+K are accepted as pairs. Allow me to call them strict pairs, as opposed to the above mixed pairs.
, J+J, Q+Q, K+K are accepted as pairs. Allow me to call them strict pairs, as opposed to the above mixed pairs.
There are 13 ranks of 4 cards each. Each rank contributes C(4, 2) = 6 pairs. Total strict pairs: 13 * 6 = 78. Probability to get a mixed pair: 78 / 1326 = 5.9%.Total strict pairs = 78 2-card hands (5.9%, but...).
However, not all blackjack pairs should be split; e.g. 10+10 or 5+5 should not be split, but stood on or doubled down. Only around 3% of strict pairs should be legitimately split. See the optimal split pairsblack jack strategy card.5. Free Blackjack Resources, Basic Strategy, Casino Gambling Systems
- Blackjack Mathematics Probability Odds Basic Strategy Tables Charts.
- The Best Blackjack Basic Strategy: Free Cards, Charts.
~ All playing decisions on one page — absolutely the best method of learning Blackjack Basic Strategy (BBS) quickly (guaranteed and also free!) - Blackjack Gambling System Based on Mathematics of Streaks.
- Blackjack Card Counting Cult, Deception in Gambling Systems.
- The Best Blackjack Strategy, System Tested with the Best Blackjack Software.
- Reality Blackjack: Real, Fake Odds, House Advantage, Edge.
Back to Forums IndexSocrates HomeSearch